Mathematical modeling of infectious diseases spreading has experienced a deep evolution during the last years, as a consequence of the application of novel theoretical developments to the description of relevant data of unprecedented levels of detail.
On the one hand, networks theory has provided epidemiologists new, strong theoretical tools to achieve a better understanding of the relationship between human populations and their susceptibility to disease. Analyzing the structural properties of human societies and their geographical distribution have revealed key aspects needed for improving epidemiological forecast capabilities. Aspects like the structure of the contact networks within and between cities, the mobility patterns of individuals or even their eventual behavioural responses against disease have been thoroughly studied, and their influences on overall disease spreading, addressed.
On the other hand, relevant real data on all these questions and many others have been rendered available to the research community. This includes curated datasets of commuting and air-transportation networks, surveys about social (and sexual) contact patterns of real populations and also detailed phylogenetic data about host and pathogen heterogeneities for many pathogens. This relatively recent availability of information has derived in the development of data-driven epidemic models able to bring theoretical developments to more specific scenarios, closer to epidemiological and clinical research.
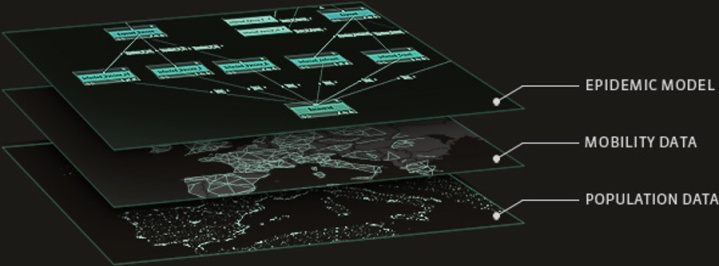
Scheme of GlEaM (Global Mobility and Epidemic model), by Balcan et al. for influenza spreading modelization. The scheme illustrates how, for a description of the disease dynamics on a global scale to be achieved, three aspects must be simultaneously taken into account: demography, mobility and natural history of the disease (epidemic models). Source.
However, most of these advances have been used to describe short-cycle diseases, i.e. those for which the typical infectious periods are much shorter than individuals life expectation. Other diseases, however, are persistent, which means that they present periods of latency that can be very large, up to such a point that, in cases like that of tuberculosis, only a fraction of infected individuals develop the disease within their lifetime. One of my main interest is indeed the development of mathematical models of spreading of persistent diseases, incorporating new ingredients, classically disregarded in the field, but already common in spreading models of short-cycle disease like influenza. the study of concepts like the coupling between disease’s dynamics and the demographic evolution of the populations, the structure of the networks of contacts relevant for disease spreading, the heterogeneity of the fitness of host-pathogen interactions and many others will derive in a relevant improvement on our understanding of the spreading mechanisms. The final goal of this research program is the development of models and analysis tools of increasing predictive skills and reliability.
The contents in this website are licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Joaquín Sanz 